

에이전트의 목표는 한 에피소드 내에서 얻을 수 있는 모든 감가된 보상의 총합(리턴값)을 최대화 하는 action의 집합을 찾는 것이다.

강화학습의 에이전트는 1.순차적이면서(<-> 단일 행동) , 동시에 2.평가 가능하고(<-> 지도학습), 3.샘플링이 가능한 피드백(<->데이터가 적음)을 학습한다.
먼저 순차적인 문제를 어떻게 분류하는지 살펴본다.

순차적인 결정 문제는 learning, planning 두 가지로 나눌 수 있다.
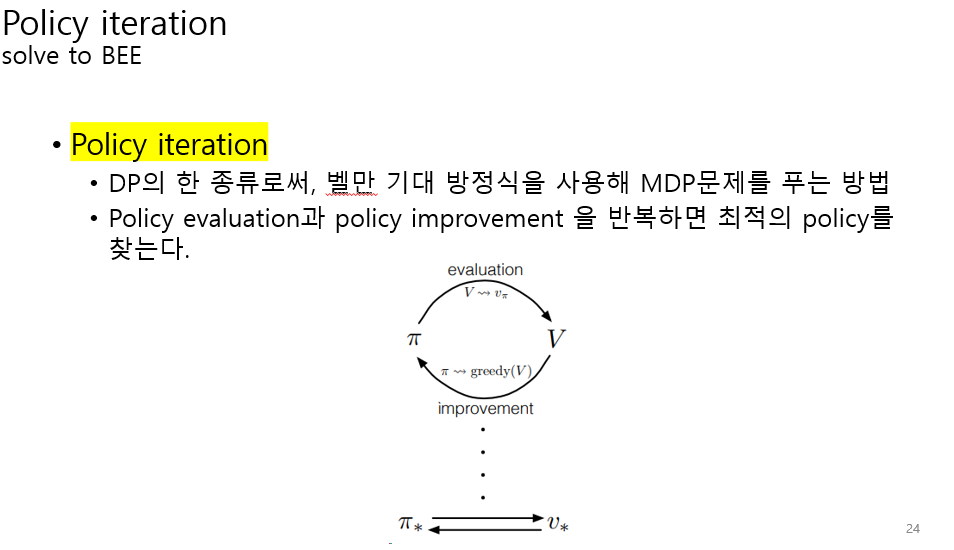
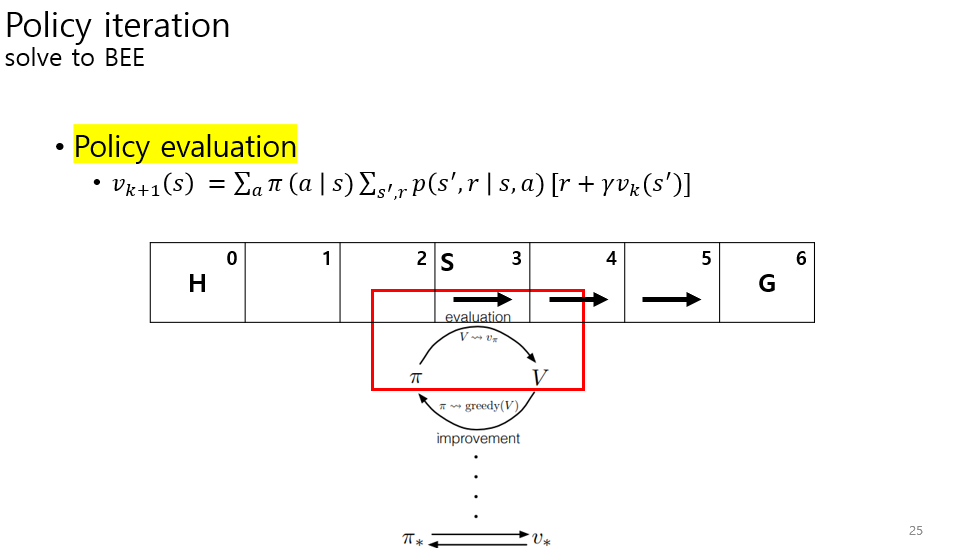
learning은 MDP가 주어지지 않을 때, 에이전트가 action을 좋고 나쁨을 판단해서 자신의 policy를 개선하는 방법론이다.
planning은 MDP가 주어졌을 때, 에이전트가 action에 대한 최적의 policy를 찾는다.
먼저 planning의 예제를 살펴본다.
Planning
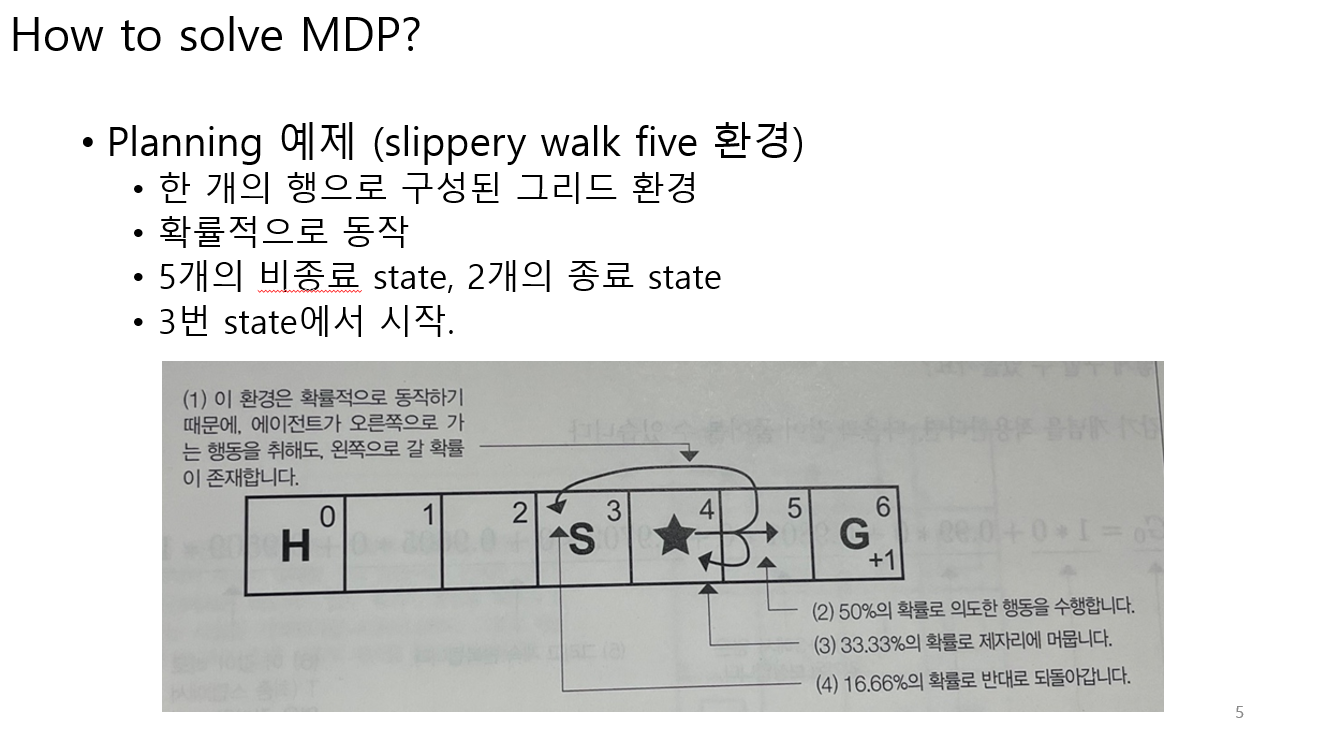
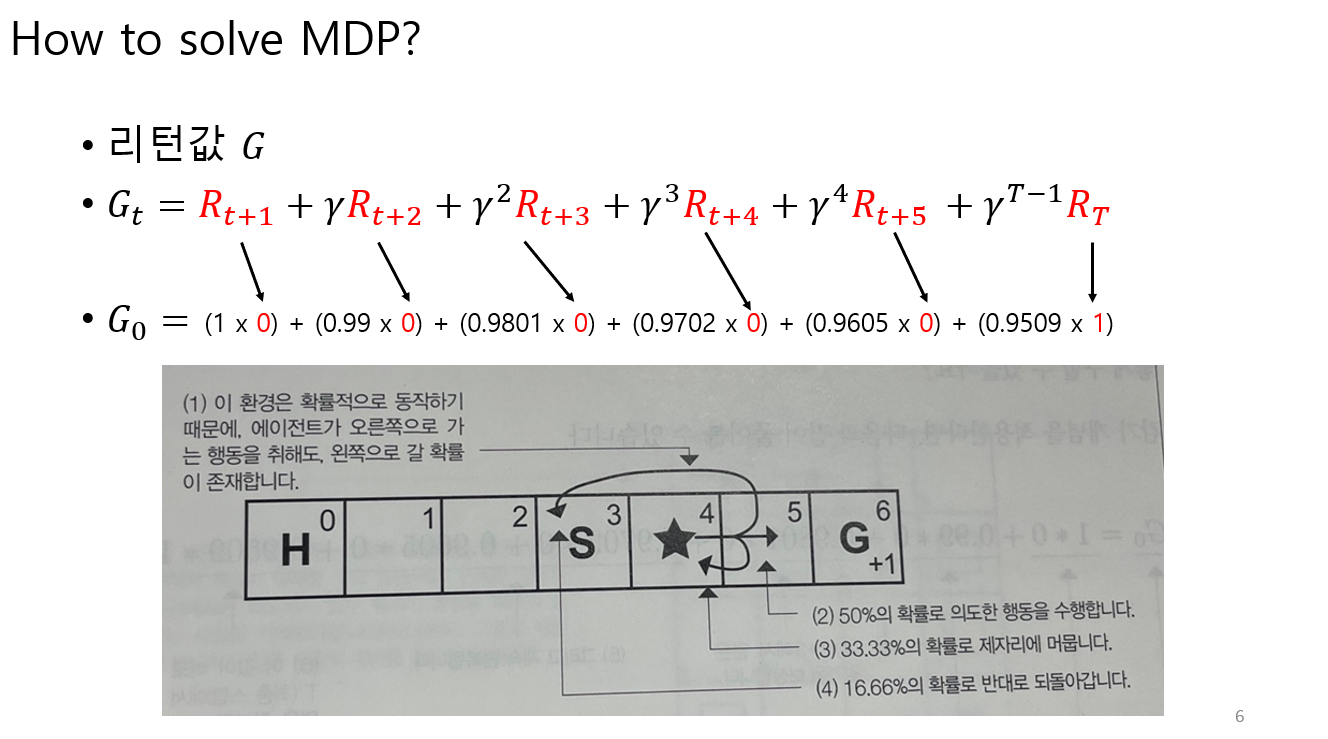
MDP가 주어졌을 때, 리턴 값을 계산해본다. 이때 미래보상에 대해서는 감가된 리턴으로 계산한다.

최적의 policy으로 가는 action 집합을 찾는다. 어떻게 찾을까?

deterministic(<->stochastic) 한 환경안에서 에피소드가 수행한 모든 action의 집합(plan)만으로는 어떤 action이 보상을 최대로 받을 수 있는지 비교할 수가 없다.
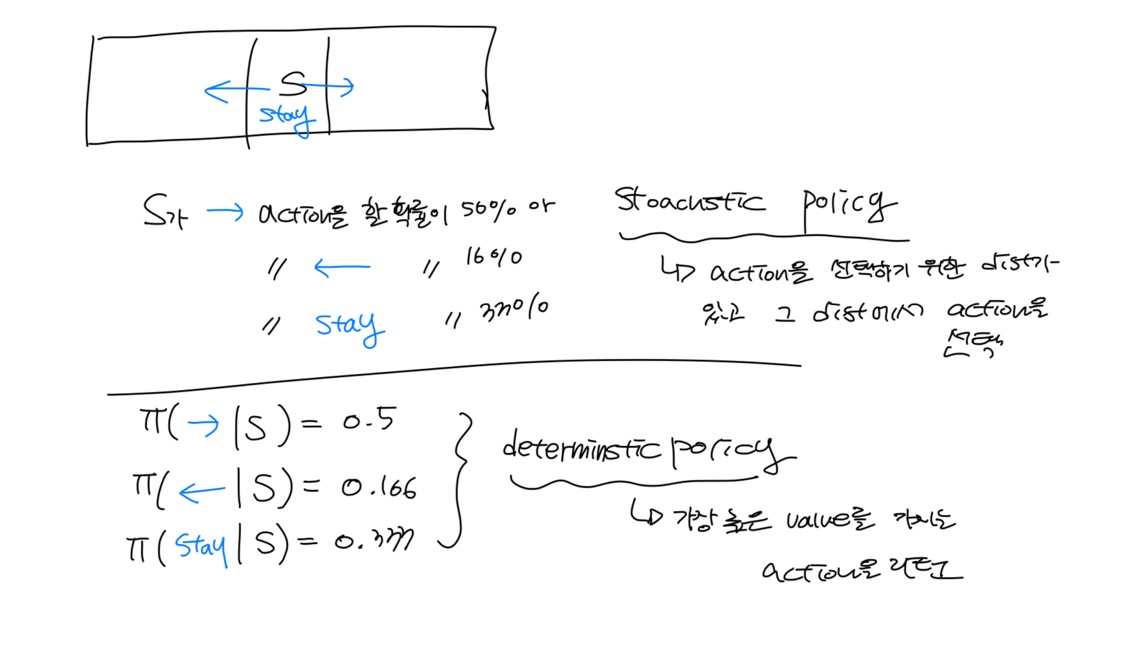

그래서 policy가 등장한다.
policy는 모든 발생 가능한 state를 수행한 action들의 집합이다.
그렇다면 어떤 policy가 이상적인지 어떻게 비교할 수 있을까?
먼저 리턴 값만으로는 판단이 불가능하다.
에이전트가 리턴값이 큰 plan을 수행할 수 있다는 보장이 있을까?
action이 이상적인지는 알아도 환경이 에이전트가 목적지로 가려는 행동과 반대로 행동 할 수도 있다.(노이즈 영향)
그래서 에이전트는 리턴의 기댓값을 최대화 하는 방법으로 action들의 집합을 찾는다.
Learning

learning은 MDP가 없다는 가정하에 에이전트가 환경과 상호작용을 통해서 어떤 action이 좋고 나쁜지를 배운다고 했다.
action이 좋고 나쁨을 판단할 때, 에이전트는 리턴의 기댓값을 최대화 하는 방법으로 action들의 집합을 찾는다(policy를 개선한다).

MDP가 주어지지 않는다는 것은 환경의 전이 P(transition matrix)와 reward function이 주어지지 않을 때이다.

에이전트가 취한 action의 집합들이(policy) 얼마나 좋은지 판단하는 지표는 위와 같이 3가지로 분류한다.

에이전트가 리턴 값을 계산하기 위해서는 한 에피소드가 끝나야지 계산이 가능하다.
value function은 한 에피소드가 끝나기 전에 미래에 받을 리턴 값을 예측하는 함수이다.
위의 이미지에는 보상이라고 했지만 리턴 값이 더 올바른 표현이다.

value function의 입력은 state, 출력은 앞으로 받을 리턴의 기댓값이다.


value function은 현재 state에서 얼만큼의 보상을 받을 수 있는 지 계산 한다. 이것을 좀 더 자세하게 생각하면
현재 받을 수 있는 보상(Rt+1) + 미래에 받을 수 있는 보상에 discout factor가 곱해진 값(감마*v(St+1))
을 계산해서 출력한다.
아래 이미지는 예시를 들어서 더 자세하게 설명한다.

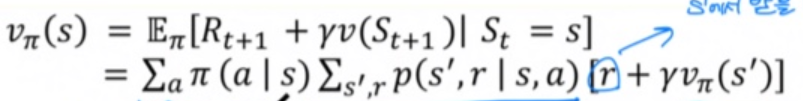
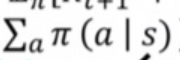
policy pi를 따르면서 현재 state s에서 action a가 발생할 수 있는 확률이다.
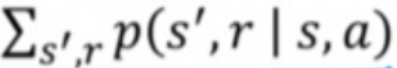
state s, action a가 주어졌을 때 다음 state s', r가 발생할 확률이다.
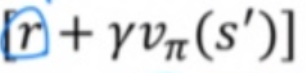
r은 s'에서 즉시 받을 수 있는 보상이고
감마텀은 s'에서 미래에 받을 수 있는 리턴값의 기댓값이다.
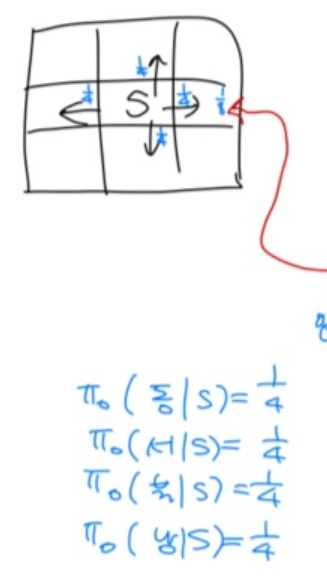
현재 policy는 총 4개의 action이 발생할 확률을 각각 1/4로 설정.
이 policy에서 나올 수 있는
discount factor는 0.9로 고정한다. (실제로는 계속 값이 변하지만 일단 편의를 위해 고정)
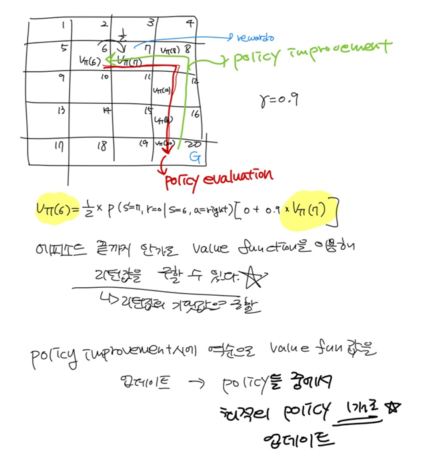
6에서 얼만큼의 보상을 받을 수 있는지 계산하면

현재 state 6에서 각각 모든 action을 취했을 때 다음 state 에서 보상 r이 발생할 확률과
현재 state 6에서 취할 수 있는 action의 확률이 필요하다.
여기에서 random variable은 s',r, a이다.

현재 state 6에서 취할 수 있는 모든 action들에서 나올 수 있는 모든 리턴을 action의 갯수로 나누어 기댓값을 구한다.
현재 state 6의 value를 구하기 위해서는 그 다음 state 7의 value가 필요하다. 즉 재귀적으로 계산 가능하다.

이러한 수식을 벨만기대방정식이라고 부른다.
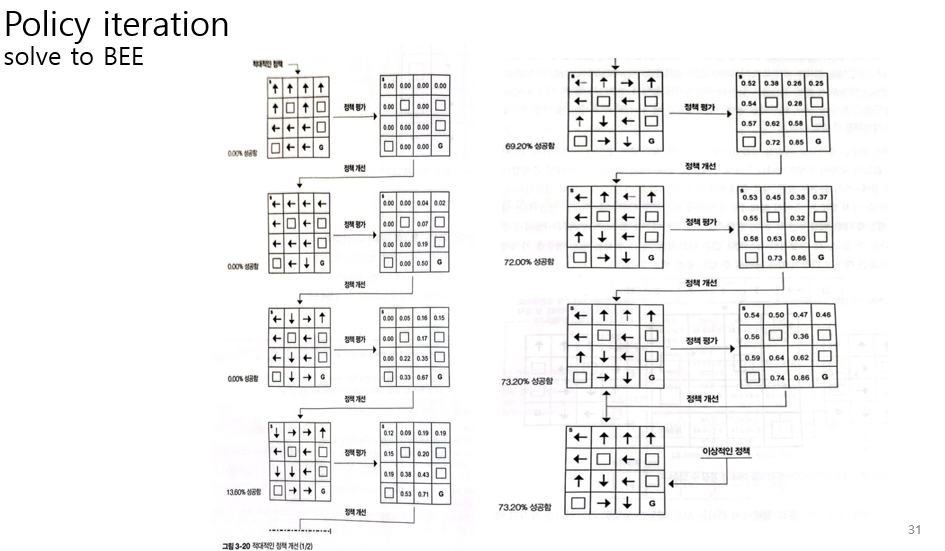
이 방정식을 풀면 모든 state에 대한 리턴의 기댓값을 구할 수 있다.
결국 강화학습에서는 리턴을 최대화하는 action들의 집합을 찾는 것이다.
벨만기대방정식을 풀어서 리턴의 기댓값을 구하고
나중에 이 리턴의 기댓값을 통해 최적의 action들의 집합을 출력한다.


Q 함수는 위에서 설명했던 V함수와 달리 MDP없이 policy를 개선한다.
V함수에서 MDP가 필요한 이유는 action이 주어지지 않기 때문이다.
V함수는 action이 주어지지 않으므로, 모든 action에 대해서 평균을 내는식으로 계산했다.
하지만 Q함수는 action이 주어지므로 모든 action에 대한 평균을 내지 않는다.
action이 주어지므로 transition을 구할 수 있다.
transition은 에이전트의 특정 action을 취했을 때 어떤 state로 변하는지를 나타내는 함수이다.


벨만 최적 방정식은 현재 state에서 보상이 최대인 value function이다.









'인공지능 > 강화학습' 카테고리의 다른 글
| [심층 강화학습] DDPG(Deep Deterministic Policy Gradient) (0) | 2024.02.27 |
|---|---|
| [그로킹 심층 강화학습] - ch1 심층 강화학습의 기초, ch2 강화학습의 수학적 기초 (4) | 2024.01.12 |

