Discriminative VS Generative

Discriminative learing algorithms은 입력 데이터 x가 주어졌을 때, 정답 레이블 y를 예측할 수 있도록 학습하는 알고리즘이다.
예시로 logistic regression이 있으며, 수식은 다음과 같이 표현한다. $$ p(y|x; \theta) $$
Generative learing algorithms은 정답 레이블 y가 주어졌을 때, 입력 데이터 x들이 어떤 특징을 가지는 지 학습하는 알고리즘이다. 수식은 다음과 아래와 같이 표현한다. $$ p(x|y) $$
$$ p(y|x) $$ 를 Bayes rule을 이용해서 아래와 같이 풀어서 $$ p(x|y)p(y) $$를 구할 수 있다.
$$ p(y|x) = \frac{p(x|y)p(y)}{p(x)} $$
$$ p(x) = p(x|y = 1)p(y = 1) + p(x|y = 0)p(y = 0) \\ $$
$$ p(y = 1 | x) = \frac{p(x|y = 1)p(y = 1)}{p(x|y = 1)p(y = 1) + p(x|y = 0)p(y = 0)} $$
Generative learning algorithms은 $$ p(x|y), p(y) $$ 를 학습한다.

먼저 위의 식에서 첫 번째 줄은 Discriminative learning algorithms의 목적함수를 나타낸다.
Discriminative learning algorithms 목적 함수는 입력 데이터 x를 고려해 가장 가능성이 높은 정답 레이블 y값을 선택하는 것이다. 위의 식에서 두 번째 줄은 Generative learning algorithms의 목적함수를 나타낸다. Generative learning algorithms은 정답 레이블 y를 고려해 y가 가진 입력데이터 x의 feature가 무엇인지 찾는 것이다. $$argmax_y p(x|y)p(y) $$은 y값이 주어졌을 때 x를 생성할 수 있다.
이 성질을 토대로 GDA에 대해 이야기 할 수 있다. 두 목적 함수 모두 확률을 최대화 해야한다.
Gaussian discriminant analysis(GDA)
Generative learning algorithm은 먼저 Gaussian discriminant analysis(GDA)를 이용한다. $$p(x|y)는 다변량 정규분포 (multivariate normal distribution)을 따른다고 가정한다.
다변량 정규분포
다변량 정규분포는 n 차원을 가지는 정규분포이고, 다변량 가우시안 분포라고도 부른다.
그리고 mean vector, covariance matrix는 파라미터화 된다.


covariance matrix는 두 확률 변수의 상관도를 나타낸다.


단일 변수 정규분포에서 확률변수 X가 연속 랜덤변수라면 기댓값이 위의 식과 같았다. GDA에서도 동일하게 유지된다.
vector-valued 확률변수 Z는 아래와 같이 정의된다.



확률 변수 X 가 위의 식과 같은 정규분포를 따른다면, X의 covariance는 nXn차원의 매트릭스 형태로 나타날 것이다.

위의 그림에서 왼쪽 그림은 covariance matrix에서 자기자신에 대한 상관도는 1이고 두 개의 확률변수들 끼리의 상관도는 0이다.
가운데 그림은 covariance matrix를 살펴보면 자기자신에 대한 상관도는 1이고 두 개의 확률변수들 끼리의 상관도는 0.5이다.
오른쪽 그림은 covariance matrix를 살펴보면 자기자신에 대한 상관도는 1이고 두 개의 확률변수들 끼리의 상관도는 0.8이다.
참고) 공분산 행렬

GDA 모델
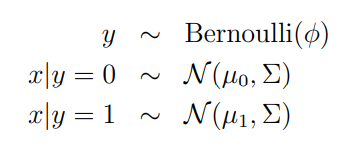

GDA모델은 정답 레이블 y=1, y=0인 경우 입력 데이터 x의 확률 밀도가 가우시안 분포를 따른다고 가정한다.

모델의 파라미터는 4개이고, 두 개의 평균 벡터들은 서로 다른 벡터를 가진다.
covariance matrix는 하나로 사용함.

$$ p( x^(i) | y^(i) ) $$를 최대화하는 파라미터 4개를 찾는 것이다.

평균 벡터 0 인 경우 y=0일 때 모든 입력 데이터의 feature를 합산 후 평균을 구한다.
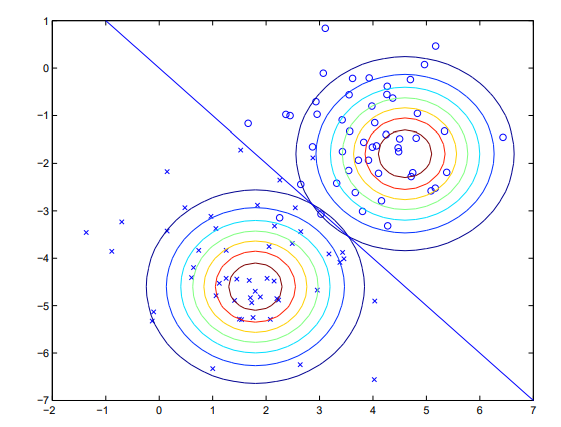
covariance가 같으므로 분포는 같지만(모형, 방향 같음) 평균은 2개의 벡터를 각각 가지게 된다.
각 레이블에 대한 가우시안 분포가 있으므로 레이블의 새로운 샘플(x)를 생성할 수 있다.
GDA와 logistic regression
GDA는 logistic regression과 관계가 깊다.
logistic regression은 아래의 수식으로 표현한다.
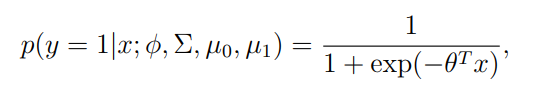
두 알고리즘은 학습 할 때 마다 다른 decision boundaries를 제공한다.
같은 데이터셋을 이용할 때, GDA와 logistic regression 중에서 어떤 알고리즘이 더 좋을까?
p(x|y)가 다변량 가우시안(covariance Σ 포함)이면 p(y|x)는 필연적으로 로지스틱 함수를 따른다고 주장한다. 베르누이 분포 데이터는 로지스틱 표현으로 표현할 수 있다.
그러나 그 반대는 사실이 아니다. 즉, 로지스틱 함수인 p(y|x)는 p(x|y)가 다변량 가우시안임을 의미하지 않는다. 이것은 GDA가 로지스틱 회귀보다 데이터에 대해 더 강력한 모델링 가정을 한다는 것을 보여준다.
데이터의 양이 많으면서 가우시안 분포를 따르는 것이 어느 정도 보장이 된다면 GDA가 더 효과적이다.
그러나 데이터가 가우시안 분포를 따르지 않으면서 데이터 양이 많아지면 logistic regression이 GDA보다 성능이 좋다.
예시로 포아송 분포의 경우 logistic regression은 잘 수행되지만 GDA에서는 작동이 제대로 되지 않는다.
그렇기 때문에 대부분의 경우 GDA가 아닌 Discriminative learning algorithms을 사용한다.
참고
https://sanjivgautamofficial.medium.com/generative-learning-algorithms-8a306976b9b1
Generative Learning Algorithms
Andrew NG. So much likely I would be overwhelmed.
sanjivgautamofficial.medium.com
https://blog.naver.com/justinbin/222988389603
Generative Learning Algorithm
지금까지의 포스팅에서 다뤘던 regression algorithm들은 input variable x와 output variable y의 dataset...
blog.naver.com
https://see.stanford.edu/materials/aimlcs229/cs229-notes2.pdf
'인공지능 > 머신러닝' 카테고리의 다른 글
| [Pandas] Shape of passed values is (598, 2795), indices imply (598, 2877) error (0) | 2023.02.08 |
|---|---|
| 파라미터와 하이퍼파라미터 (train 하는가? 안하는가?) (2) | 2023.01.19 |
